Aufgabe B 1
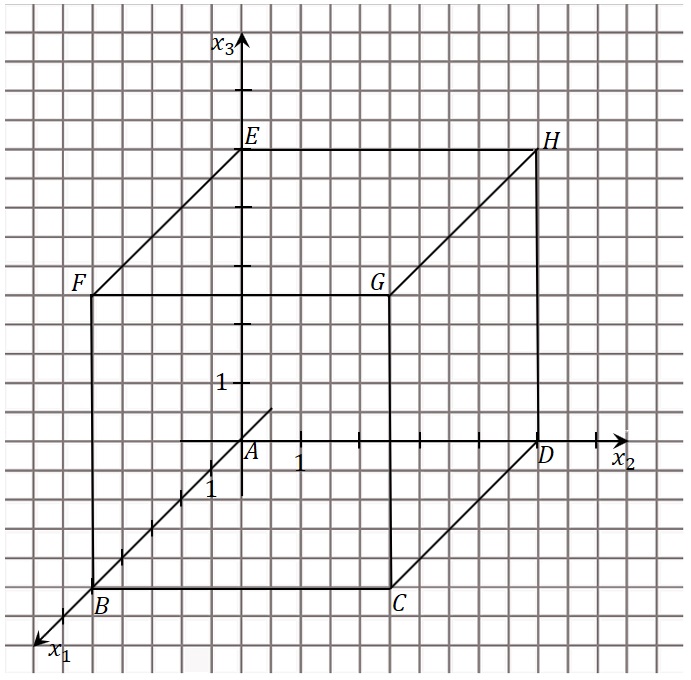
Die Abbildung in der Anlage zeigt den Würfel ABCDEFGH mit A(0|0|0) und G(5|5|5) in einem kartesischen Koordinatensystem.
Die Ebene T schneidet die Kanten des Würfels unter anderem in den Punkten K(5|0|1), L(2|5|0), M(0|5|2) und N(1|0|5).
a) Zeichnen Sie das Viereck KLMN in die Abbildung ein.
Zeigen Sie, dass das Viereck KLMN ein Trapez ist und zwei gleich lange Seiten hat.
Ermitteln Sie eine Gleichung der Ebene T in Koordinatenform.
Geben Sie die Koordinaten des Schnittpunktes von T mit der x1-Achse an.
(Teilergebnis: T: 5x1+4x2+5x3=30)
(5 VP)
b) Die Spitze einer Pyramide mit der Grundfläche KLMN liegt auf der Strecke FG.
Untersuchen Sie, ob die Höhe dieser Pyramide
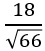betragen kann.(2 VP)
c) Betrachten wir die Schar der Geraden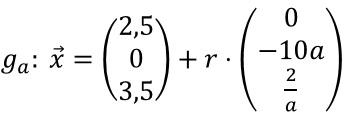
mit a>0.Begründen Sie, dass keine Gerade der Schar in der Ebene mit der Gleichung x3=3,5 liegt.
Gegeben ist die Ebene U: -5x1+4x2+5x3=5.
Untersuchen Sie, ob die Schnittgerade von T und U zur betrachteten Schar gehört.
(3 VP)
| Downloads |
PowerPoint